Understanding statistics has never been more important for the practice of medicine. Unfortunately, innumeracy plagues the medical field. Listen to Episode 15 of Bedside Rounds to learn more, and maybe find a way out of this statistical morass with this one weird trick…

If you ever sit through a medicine case discussion, you can be forgiven in thinking that medicine is about numbers and not people. I recently made my wife sit through a multi-continent discussion on an unusual presentation of nephrotic syndrome (a protein-spilling kidney disease). “It’ll be interesting!” I insisted, and I thought it was — but from her perspective, it was a list of about 80 constantly changing laboratory values, and a debate on the test characteristics of urine dips and kidney biopsies.

4+ proteinuria, or beer? Either way, it’s hard to miss.

Medicine focusing on laboratory values is nothing new. As early as two decades after the first lab test was invented, in the halcyon 1920s, Francis Peabody noted that his medical residents were increasingly substituting lab tests for clinical judgement, writing, “Good medicine does not consist in the indiscriminate application of laboratory examination but rather in having a clear comprehension of the probabilities of the case as to know what tests might be of value.” And a quick note about Dr. Peabody, because you’re probably never heard of him, but you’ve certainly heard his famous quote: “The secret of the care of the patient is in caring for the patient.” He was a humanitarian and obsessed with patient-focused care a half-century before the phrase existed, and so dedicated to medicine that as he lay dying of cancer at the age of 46, he found the time to pen a case-report on the effects of morphine on his body.

“”The treatment of a disease must be completely impersonal; the treatment of a patient must be completely personal.” HT to Harvard Medical School.

So by the 1920s it was becoming clear that laboratory (and later diagnostic and imaging) testing was becoming increasingly important in the care of patients. But it wasn’t until 60 years later that we finally started to test how much physicians understood interpretation of the numbers we so relied on. One of the classic studies was published by Don Berwick, who would later form the Institute of Healthcare Improvement and run the Centers for Medicare and Medicaid Services for President Obama, back in 1982, entitled “When Doctors Meet Numbers.” Essentially, the subtitle should have been “It Doesn’t Go Well,” because the study found a significant lack of familiarity and understanding of basic statistical principles. Most concerningly,there was an inverse relationship between time from graduation and statistical performance, with career physicians in the community doing the worst.

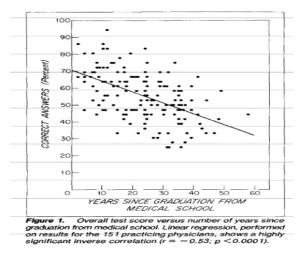
Figure 1! Fun fact: I had lunch with Dr. Berwick once in medical school. I sure hope he doesn’t remember me, because I also had grown a ridiculous mustache for a Halloween costume.

The ensuing decades saw the prominence of preventative medicine, and the stakes of understanding numbers only increased. Now physicians have to interpret screening tests and primary prevention of diseases that affected an entire population — who should get a mammogram, whether you should take that statin, and which vaccination to give to which patient. Unfortunately, doctors still showed a significant misunderstanding of statistics. A study in 2012 surveyed hundreds of primary care doctors on two cancer screening tests, and asked which they would recommend to patients. The first improved five-year survival from 68% to 98%, and the second decreased mortality from 2.0 to 1.6 deaths per 1000 persons. Over two-thirds recommended the first test, and only 20% recommended the second. The problem, of course, is that both tests were really the PSA (prostate-specific antigen) test for prostate cancer. Furthermore the first statistic is meaningless — increased survival from a screening program probably represents lead-time bias; the second statistic, actual mortality benefit, is what we should care about. And to be clear — patients make potentially life-changing decisions based on their physician’s understanding of these statistics. Sometimes it can even influence policy of an entire country — Rudy Giuliani, for example, when he was running for president in 2012 mocked the UK’s  “socialized medicine” prostate cancer “death rate”, conflating survival from a lead time bias with mortality, when in fact mortality from prostate cancer in the the US and UK are essentially the same.

Which brings me to one of my favorite studies on physician innumeracy, mostly because it can be easily replicated. So let’s do some math!

With the Olympics just over, let’s say you’re a member of the International Antidoping Agency, and you’ve been tasked with screening athletes for abusing recently-banned meldonium. A tall task, but you have some help — you have a new urine screening test that has a false positive rate of five percent. You also know that from previous surveys of international athletes about one in a thousand have used the drug for performance enhancement. So armed with this data — a prevalence of 1 in a 1000, and a false positive rate of 5% — you confront an American swimmer who has just tested positive for meldonium. He insists his innocence. With your superior knowledge of biostatistics, what are the chances that he is telling the truth? Or stated another way, what are the odds that this positive is a true positive, and not a false positive?

Meldonium, used by elite athletes with heart conditions everywhere.

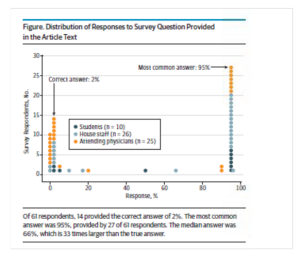
This study was first performed — sans the doping example — in 1979 by Dr. Cascells at Harvard. He found that only 18% of medical students, residents, and attendings got the right answer. The average risk was over-estimated by 57%. His study was repeated in JAMA in 2014 with the same cohort, and no change of the results. And more recently, yours truly performed the same experiment on his co-residents for a graduation project, and again, no change of the results.

So what is the right answer? The most common answer is 95% for understandable reasons — 5% false positive means that 95% will be true positives, right? — but in fact, the chance that the swimmer is lying is only 1.96%. He is almost certainly telling the truth, and the test is a false positive. The short answer why is that positive predictive value (proportion of all positives that are true positives) is based on prevalence. For the longer answer, keep listening.

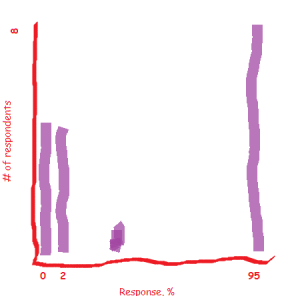
One of these graphs was made my a major medical journal. The other was made by me. Can you tell which one?

All of which brings me to the famous paraphrase of HG Wells, that “statistical thinking will one day be as necessary for efficient citizenship as the ability to read and write.” I tend to agree with him about citizenship, but there’s no question that efficient doctoring also requires statistical thinking. So how do we correct doctors’ innumeracy? Every think piece in the journals decrying innumeracy have the same answer: education. Maybe we should drop calculus from premed requirements in favor of statistics. What about more stats in med school? Residency? Maybe for continuing medical education? All sound life great ideas — with the major caveat being that it doesn’t seem to work. Even Francis Peabody, back in 1922, closed his article on over-reliance of laboratory testing by recommending more statistical training. If 100 years of recommending more training hasn’t worked, what will? Or are we all just screwed?

Amen H.G. Wells! (even if he didn’t really write it…)

Of course not! I’m forever an optimist, and not to get too clickbaity on you, but there’s this one weird trick that might fix all our problems — and it’s called natural frequency.  This is the pet project of Gerd Gigerenzer — apologies for butchering the German — a cognitive psychologist at the Max Planck Institute in Germany, and his ideas have already started to transform how we talk about preventative medicine with patients. I don’t want to get too much into the weeds, but basically Dr. Gigerenzer states that humans have a fundamental understanding of statistics when we talk about them in terms of natural frequencies, but not when talking about conditional probabilities. Normal biostats is “conditional” — the population, or denominator, isn’t the same. So with sensitivity, I’m talking about only patients who have a condition. With positive predictive value, I’m just talking to those carrying a positive test. And to top it all off, with prevalence I’m including everyone. This is the reason that the doping example is so confusing. In natural frequencies, we use the same “denominator” — we talk about the same population.

Clickbait… the future of Bedside Rounds!

So let’s reframe the original question. Out of a thousand athletes, one is doping, fifty (5% of 1000) will have a positive test but be clean, and the other 949 will be clean and also test negative. What you want to know is, out of those who test positive, how many will actually be doping? When stated like this, it’s easy to see — 51 will be positive, and one will actually be doping. So 1/51, or 1.96%.

Figure 1: Prevalence. Orange dot is the one doper, 999 black dots (I counted ’em!) are the non-dopers. Figure 2: False positive rate. One positive doper, 50 positive non-dopers, 949 negative non-dopers. Figure 3: One positive doper out of 51 positives == 1/51! C’est voila!

Gigerenzer has done multiple studies where he provides physicians with information on a screening or laboratory test, first in conditional probabilities, like I did initially, and then using natural frequencies. And guess what — in every example, physicians’ understanding improves dramatically. Major healthcare organizations have taken note. Cornell has an online tool called BreastScreeningDecisions.com that uses a woman’s own risk profile and natural frequencies to show the risks and benefits of mammography. The Mayo Clinic has developed natural frequencies to help with the decision to prescribe aspirin and statin medications. And Kaiser — who I had the pleasure of working with during my residency — has even built natural frequency decision aids into its Electronic Medical Record. All these links are on the website, by the way.

So what are we doctors to take from this? One of the biggest things, I think, is to be cautious. When we start talking probability, slow down, recognize we’re talking about conditional probability, and proceed with caution. But I also think it can change how we communicate risk with our patients. That includes decisions aids, but also a more fundamental shift on how we discuss risk. I’ve told plenty of patients something like, “Citalopram has a 20% rate of sexual dysfunction”. This is the classic “20% chance of rain” problem. Does that mean 20% of sexual encounters will have some sort of problem, and we’re just rolling the dice? Or will sex be 20% more, er, dysfunctional? But let’s reframe it as a natural frequency, so patients know what population I’m talking about. How about, “If I treat 10 patients with citalopram, two of them will develop sexual dysfunction”? We might not understand 20%, but we can understand that.

Serious people have spent a lot of time thinking about “20% chance of rain”. Of course, if we say, for 1000 days like tomorrow, in 200 of them it will rain, people understand much better. For more, http://www.npr.org/2014/07/22/332650051/there-s-a-20-percent-chance-of-rain-so-what-does-that-mean

Sources:

• Strogratz, Steven. Chances Are. NYTimes: http://opinionator.blogs.nytimes.com/2010/04/25/chances-are/?_r=0
• Berwick D, et al. When doctors meet numbers. Am J Med. 1982; 71(6):991-998.
• Cascells W, et al. Interpretation by physicians of clinical laboratory results. N Engl J Med. 1978, Nov 2;299(18):999-1001.
• Gigerenzer G. Simple tools for understanding risks: from innumeracy to insight. BMJ. 2003 Sep 27; 327(7414):741-744.
• Manrai A, et al. Medicine’s uncomfortable relationship with math. JAMA Intern Med. 2014;174(6):991-993.
• Mower, V. What we don’t know can hurt our patients. Ann Intern Med. 2012;156(5):392-393.
• Peabody GW. The physician and the laboratory. Boston Med Surg J. 1922;187:324–327.
• Wegwarth O, et al.  Do physicians understand cancer screening statistics? A national survey of primary care physicians in the United States. Ann Intern Med. 2012; 156.340-9

Music credit:

• John Williams’ Olympic Theme
• Danger Storm, Spy Glass, and Thief in the Night, by Kevin Macleod, incompetech.com